

SFC یا نمودار تابع ترتیبی (Sequential Function Chart) یک زبان برنامهنویسی گرافیکی است که در میان زبانهایی قرار دارد که توسط استاندارد IEC 61131-3 برای برنامهنویسی سیستم های DCS و PLC با استفاده از منطق نردبانی (Ladder Logic) شناسایی و تعریف شدهاند.
نمودارهای SFC، یا نمودارهای تابع ترتیبی (Sequential Function Charts)، زبانهای برنامهنویسی مبتنی بر متن نیستند، بلکه زبانهای برنامهنویسی بصری هستند که مشابه فلوچارتهای مورد استفاده برای الگوریتمهای علوم کامپیوتر میباشند.
SFCها معمولاً در سناریوهایی استفاده میشوند که در آنها چندین حالت عملیاتی وجود دارد و نمایش آنها آسانتر است. مزیت برنامهنویسی SFC توانایی آن در کمک به مهندس برای تقسیم فرایندهای بزرگ و پیچیده به بخشهای کوچکتر است تا بهراحتی قابل درک باشند.
در PCS 7 (سیستم DCS شرکت زیمنس)، برنامهنویسی با SFC کاربرد گستردهای دارد، بهویژه برای کنترل فرایندهای ترتیبی و پیچیده.
در سیستمهای کنترل توزیعشده (DCS)، برنامهنویسی با استفاده از نمودار تابع ترتیبی (SFC) نقش بسیار مهمی در مدیریت و کنترل فرایندهای پیچیده دارد. SFC امکان نمایش بصری توالی عملیات، انشعابها، و همگراییها را فراهم میکند و به مهندسین اجازه میدهد که سیستمهای بزرگ و چندمرحلهای را بهصورت گام به گام طراحی، شبیهسازی و کنترل کنند.
مزایای استفاده از SFC در DCS عبارتاند از:
در کل، استفاده از SFC در سیستمهای DCS به مهندسین اجازه میدهد تا فرایندهای پیچیده را بهصورت منطقی، منظم و قابل کنترل طراحی کنند، و همزمان قابلیت مشاهده و پیگیری عملیات در زمان واقعی را فراهم میسازد.
برنامهنویسی SFC چگونه کار میکند؟
کنترلهای ترتیبی شامل پردازش عملیات ترتیبی و موازی هستند که از نظر زمان یا رویدادها گسسته میباشند و عمدتاً برای کنترل توالیهای فرایندی پیچیده به کار میروند. زبان برنامهنویسی SFC مشاهده و طراحی سیستمهای ترتیبی پیچیده را آسانتر میکند. در این زبان برنامهنویسی، عملیات بهصورت گامهای جداگانه توصیف میشوند که بهصورت ترتیبی به یکدیگر متصل هستند.
نمونهای از این اتصال ترتیبی را میتوان در عملکرد یک ماشین لباسشویی مشاهده کرد. هنگامی که یک برنامه روی ماشین لباسشویی انتخاب میشود، دارای چندین مرحله است که یکی پس از دیگری اجرا میشوند. وقتی یک مرحله به پایان میرسد، مرحله بعدی بهطور خودکار آغاز میشود. اصطلاحات «گامها (steps)» و «حالت (state)» در برنامهنویسی SFC نمایانگر یک مفهوم یکسان هستند.
در برنامهنویسی SFC، حالتها یا گامها با جعبههای مستطیلی نمایش داده میشوند. یک خط عمودی مستقیم stepهای مختلف را به یکدیگر متصل میکند و هر گام دارای خروجی متناظر خود است. بین گامها یک شرط انتقال (transition condition) وجود دارد. شکل ۱ در زیر، نمودار کلی نمودار تابع ترتیبی را نشان میدهد.

اولین step نشاندهنده آغاز عملیات است. دو حالت توسط یک خط عمودی به یکدیگر متصل میشوند. خطوط افقی بین step ها نشاندهنده شرایط انتقال (transition conditions) هستند. گاهی اوقات، شرایط انتقال میتوانند بهصورت یک مستطیل بسیار کوچکتر که بین حالتهای بزرگتر قرار دارد نمایش داده شوند.
پس از آنکه یک گام کامل شد، فرایند تنها در صورتی به حالت بعدی منتقل میشود که شرط یا شروط انتقال نیز برآورده شده باشند.
هر یک از حالتها همچنین دارای خروجیهای متناظر خود هستند. خروجیها بهصورت جعبههای مستطیلی نمایش داده میشوند که بهصورت افقی به حالت مربوطه خود متصل شدهاند.
برای هر SFC باید دو شرط رعایت شود:
هر نمودار SFC را میتوان با منطق لدر (Ladder Logic) معادلسازی کرد. شکل ۲ یک نمونه از این موضوع را نشان میدهد.
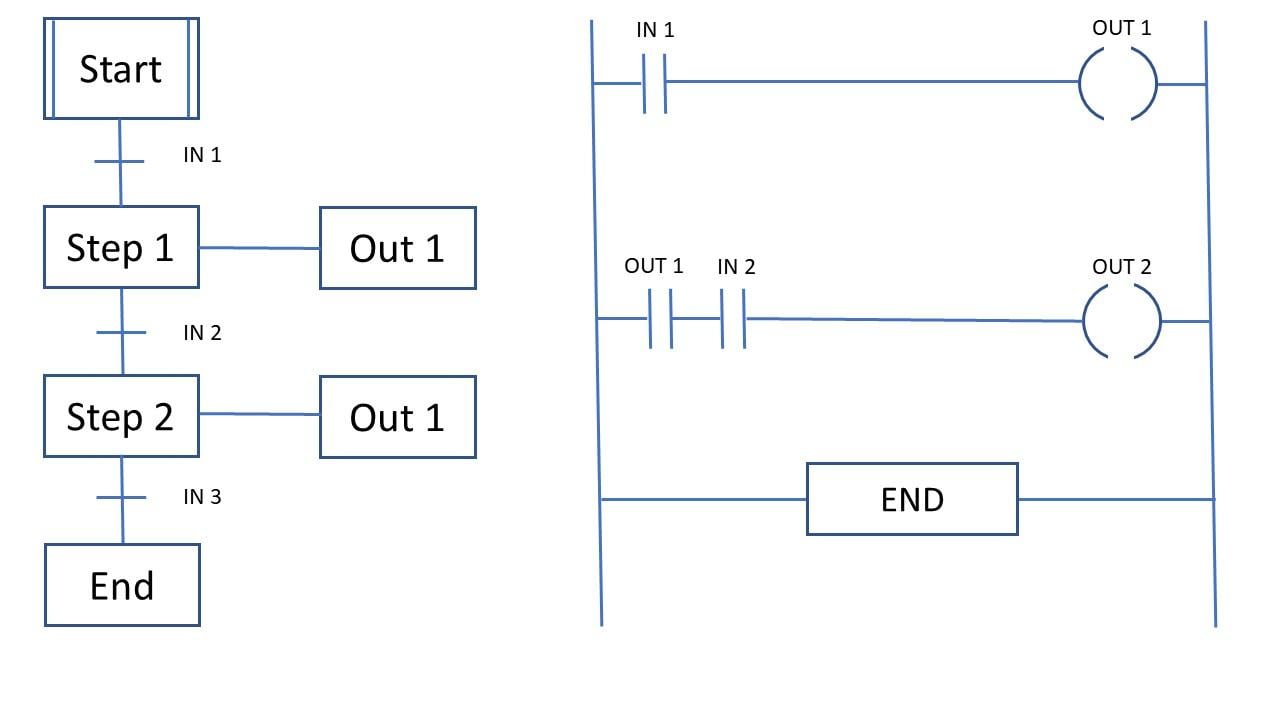
شکل ۲. نمودار SFC که با منطق لدر (Ladder Logic) معادلسازی شده است.
اولین رانگ (rung) لدر معادل step 1 است. تنها در صورتی که IN 1 رخ دهد، OUT 1 نیز فعال خواهد شد. رانگ دوم معادل گام ۲ است. تنها در صورتی که OUT 1 و IN 2 رخ دهند، OUT 2 فعال خواهد شد.
میتوان SFCها را بهصورت ترکیبی از موارد زیر خلاصه کرد:
خطوط عمودی بین گامها را بهعنوان مسیرهایی از حالت قبلی به حالت بعدی در نظر بگیرید. SFC امکان انشعاب مسیرها را به دو روش فراهم میکند: انتخابی (Selective) و موازی (Parallel). تفاوت بین این دو در محل قرارگیری شرایط انتقال نهفته است.
انشعاب موازی اجازه میدهد دو یا چند حالت بهطور همزمان رخ دهند، به شرط آنکه یک شرط انتقال واحد برآورده شود. در نمودارها، انشعاب موازی با یک جفت خط افقی نمایش داده میشود.

شکل ۳. انشعابهای موازی در SFC و نمودار نردبانی معادل آن.
پس از آنکه OUT 0 برقرار شود و شرط انتقال (IN 1) برآورده گردد، هر سه گام (گام ۱، گام ۲ و گام ۳) بهطور همزمان آغاز میشوند.
برخلاف انشعاب موازی، در اینجا همه گامهای بعدی بهصورت همزمان آغاز نمیشوند.

شکل ۴. انشعابهای انتخابی در SFC و نمودار نردبانی معادل آن.
هر گام در شاخه، شرط انتقال مخصوص به خود را دارد که باید برآورده شود. برای آغاز گام ۱، باید OUT 0 و IN 1 رخ دهند. برای آغاز گام ۲، باید OUT 0 و IN 2 رخ دهند. شرایط انتقال برای تمام گامهای بعدی مستقل از یکدیگر هستند.
همگرایی عمومی (General Convergence)
مشابه انشعاب، در برنامهنویسی SFC امکان همگرایی نیز وجود دارد. زمانی که دو یا چند شاخه دارای یک گام بعدی مشترک باشند، به آن همگرایی گفته میشود.

شکل ۵. همگرایی در SFC و نمودار نردبانی معادل آن.
در اینجا برای آغاز گام ۴، دستکم یکی از دو ترکیب باید برقرار شود. یا باید OUT 2 و IN 4 برقرار باشند، یا باید OUT 3 و IN 5 برقرار شوند تا فرایند به گام ۴ منتقل شود. اگر هر چهار شرط برقرار باشند، همان اثر را خواهد داشت. اگر OUT 2 و IN 5 برقرار باشند، برای انتقال به حالت بعدی کافی نخواهد بود، زیرا این دو شرط در شاخههای متفاوتی قرار دارند.
تفاوت همگرایی همزمان با همگرایی عمومی در این است که تنها یک شرط انتقال برای تمام حالتهای قبلی که به هم همگرا میشوند وجود دارد. اگر هر یک از خروجیها همراه با این شرط انتقال واحد برقرار شود، فرایند به گام بعدی منتقل میشود.

شکل ۶. همگرایی همزمان در SFC و نمودار نردبانی معادل آن.
شکل ۶ نشان میدهد که برای گام ۲ و گام ۳ تنها یک شرط انتقال وجود دارد. اگر هر یک از OUT 2 یا OUT 3 همراه با شرط انتقال IN 4 برقرار شود، گام ۴ فعال خواهد شد.
این مروری بر ساختار پایهای SFCها است. با این دانش، میتوان نمودارهای منطق نردبانی (Ladder Logic) را به نمودارهای تابع ترتیبی (Sequential Function Charts) تبدیل کرد و بالعکس. تبدیلهای مشابه همچنین میتوانند با نمودارهای بلوکی عملکردی (Functional Block Diagrams – FBD)، فهرست دستورالعملها (Instruction Lists – IL) و متن ساختیافته (Structured Text – ST) انجام شوند.